§ 2.3 Графические информационные модели
Сейчас мы узнаем, как превращать информацию в картинки, схемы и графы — и зачем это вообще нужно. Представь: вместо длинного текста ты смотришь на схему — и сразу всё понятно!

2.3.1. Многообразие графических информационных моделей
Представь: ты открываешь учебник физики, и там куча формул и текста. Глаза разбегаются, правда? А теперь представь ту же информацию в виде яркой схемы с картинками — сразу понятнее! Вот для этого и нужны графические информационные модели.
💡 Что это такое?
Графические информационные модели — это способ показать объект или процесс с помощью картинок, символов, стрелок и других визуальных элементов. Вместо того чтобы читать длинный текст, ты смотришь на схему — и сразу всё ясно.
Для наглядного отображения объектов используются условные графические изображения (образные элементы), зачастую дополняемые числами, символами и текстами (знаковыми элементами).

Разные способы показать информацию: схемы, карты, чертежи, графики, диаграммы
📐 Общее представление
Показывает объект в общих чертах, выделяя главное (например, схема метро или электрической цепи)
🗺️ Уменьшенное изображение
Географическая карта — уменьшенное обобщённое изображение поверхности Земли
📏 Точное изображение
Условное графическое изображение предмета с точным соотношением размеров
📈 Зависимость величин
Графическое изображение, дающее наглядное представление о характере зависимости одной величины от другой
📊 Сравнение данных
Графическое изображение, дающее наглядное представление о соотношении каких-либо величин
💡 Важно понимать
Часто бывает так, что одну и ту же вещь можно показать по-разному. Например, устройство твоего смартфона можно нарисовать как схему блоков, а можно — как детальный чертёж.
Схема — это просто!
Схема — это когда мы рисуем объект в общих чертах, выделяя главное. Например, схема метро — там нет точных расстояний и поворотов, зато сразу видно, как добраться из точки А в точку Б.
🎯 Ключевые особенности схемы
Схема — это представление некоторого объекта в общих, главных чертах с помощью условных обозначений. Схемами может быть представлен и внешний вид объекта, и его структура.
Схема как информационная модель не претендует на полноту предоставления информации об объекте. С помощью особых приёмов и графических обозначений на ней более рельефно выделяется один или несколько признаков рассматриваемого объекта.
📚 Примеры из школы
- Схема электрической цепи (физика)
- Схема скрещивания генов (биология)
- Схема исторической битвы
🌐 Примеры из жизни
- Схема метро
- Схема сборки мебели
- Карты в приложениях (2ГИС, Яндекс.Карты)
2.3.2. Графы
А теперь самое интересное — графы! Если нужно показать объекты и связи между ними, мы получаем граф. Граф состоит из вершин (это объекты) и рёбер (это связи между объектами).
🌐 Граф в соцсетях
Представь соцсеть: каждый человек — это вершина, а дружба между людьми — это ребро. Вот тебе и граф!

Неориентированный и ориентированный графы
Основные термины теории графов
Объекты графа. Могут изображаться кругами, овалами, точками, прямоугольниками и т.д.
Ненаправленная линия (без стрелки), соединяющая вершины
Линия направленная (со стрелкой). Вершина, из которой дуга исходит — начальная, куда входит — конечная
Последовательность рёбер (дуг), по которым можно перейти из одной вершины в другую
Типы графов
⭕ Неориентированный граф
Если вершины соединены рёбрами (линиями без стрелок)
Пример: граф друзей в соцсети (дружба взаимна)
➡️ Ориентированный граф
Если вершины соединены дугами (стрелками)
Пример: подписки в Instagram (подписка не всегда взаимна)
🔗 Связный граф
От любой вершины можно по рёбрам перейти к любой другой вершине
⚖️ Взвешенный граф
Вершины или рёбра характеризуются дополнительной информацией — весами
Пример: веса рёбер = расстояние между городами в км
⛓️ Цепь
Путь, в который любое ребро графа входит не более одного раза
🔄 Цикл
Цепь, начальная и конечная вершины которой совпадают
🕸️ Сеть
Граф с циклом
🚫 Ациклический граф
Направленный (ориентированный) граф, не имеющий циклов
🌉 Задача о Кёнигсбергских мостах
Давай разберём классную историческую задачку!
📖 Условие задачи
Река Преголя в центре старинного Кёнигсберга (ныне Калининград) разделяется на два рукава. В некоторых местах эти рукава соединены протоками. Благодаря одной такой протоке центр города оказался разбит на четыре части, которые со временем соединили мостами.
Известна старинная математическая задача: можно ли пройти по всем семи мостам центра Кёнигсберга, не проходя ни по одному из них дважды?
Схема мостов Кёнигсберга и её граф
✅ Решение Эйлера (1736 год)
Впервые эта задача была решена в 1736 году математиком Леонардом Эйлером, обозначившим части города точками, а соединяющие их мосты — линиями. Благодаря этому исходная задача свелась к следующей: можно ли обойти данный граф, не отрывая карандаш от бумаги, так, чтобы каждое его ребро было пройдено ровно один раз?
🔬 Правила Эйлера
Исследовав множество аналогичных графов, Эйлер установил:
- Если у графа все вершины чётные (т.е. из каждой вершины выходит чётное число рёбер), то такой граф можно обойти, не отрывая карандаш от бумаги; начинать можно в любой вершине
- Если у графа две нечётные вершины, то его можно обойти, не отрывая карандаш от бумаги; начинать надо в одной из нечётных вершин, а закончить — в другой
- Граф с более чем двумя нечётными вершинами обойти, не отрывая карандаш от бумаги, невозможно
🎓 Исторический факт
1736 год считается годом рождения теории графов, а Леонард Эйлер — её основоположником.
Определив чётность вершин A, B, C и D (все они нечётные!), ты можешь самостоятельно завершить решение задачи о мостах Кёнигсберга. Подсказка: это невозможно!
🌍 Где используются графы?
Графы как информационные модели находят широкое применение во многих сферах нашей жизни.

Графы везде: метро, соцсети, доставка, электросети
🚇 Планирование маршрутов
Дороги, метро, авиарейсы — всё это графы! Вершины — города/станции, рёбра — пути между ними
👥 Социальные сети
ВКонтакте, Instagram — это огромные графы. Ты — вершина, твои друзья — соседние вершины
🏗️ Проектирование
Можно существующие или вновь проектируемые дома, сооружения, кварталы изображать вершинами, а соединяющие их дороги, инженерные сети, линии электропередач и т.п. — рёбрами графа
📦 Логистика
По таким графам можно планировать оптимальные транспортные маршруты, кратчайшие объездные пути, расположение торговых точек и других объектов
✅ Пример 1: Считаем пути в графе
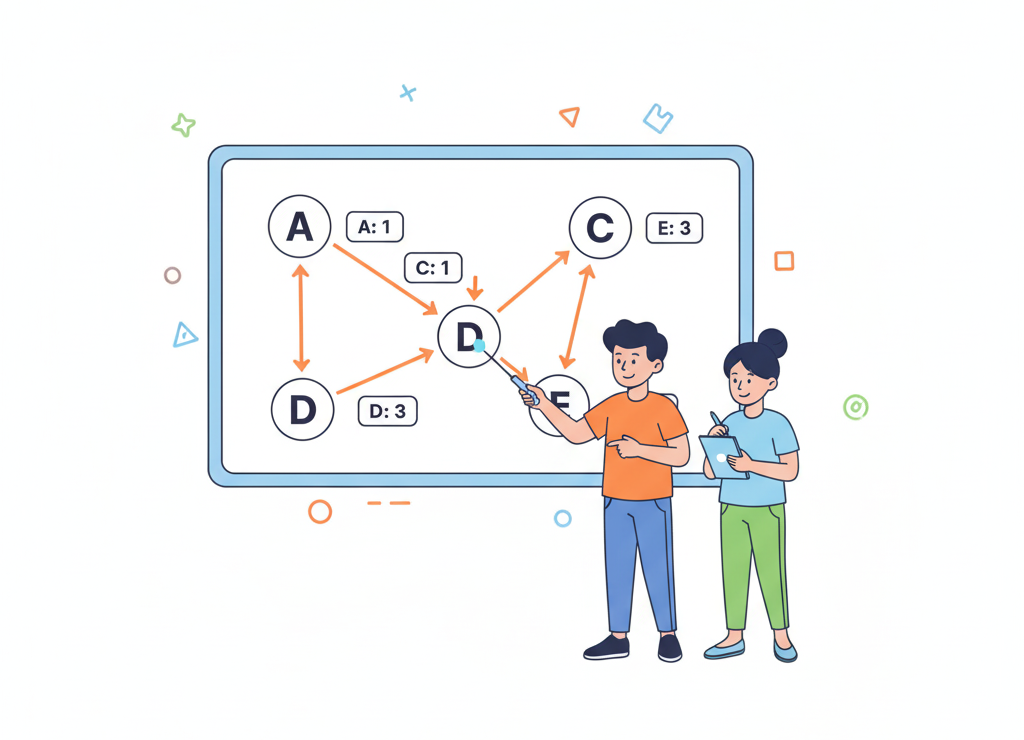
На рис. 2.13 изображена схема дорог, связывающих торговые точки A, B, C, D, E. По каждой дороге можно двигаться только в направлении, указанном стрелкой. Сколько существует различных путей от точки A до точки E?
Схема дорог (направленный ациклический граф)
🎯 Анализ графа
Граф на рисунке — направленный ациклический граф. Обратите внимание на вершину A: это единственная вершина графа, в которую не входит ни одна дуга, а все дуги из неё выходят. A — начальная вершина (источник) рассматриваемого графа.
Что касается вершины E, то есть входящие в неё дуги, но нет ни одной дуги, выходящей из неё. E — конечная вершина (сток) рассматриваемого графа.
💡 Решение
Шаг 1: В вершину E можно попасть только из вершин C и D. Если мы будем знать число путей из вершины A в вершину C и из вершины A в вершину D, то, сложив их, получим искомое число путей из A в E.
Шаг 2: В вершину C можно попасть непосредственно из вершины A и из вершины B. В свою очередь, существует единственный путь из вершины A в вершину B. Таким образом, из вершины A в вершину C можно попасть двумя путями:
1 (напрямую из A) + 1 (через B) = 2
Шаг 3: Что касается вершины D, она является конечной вершиной для трёх дуг: BD, AD и CD. Следовательно, в неё можно попасть из вершин A, B и C:
1 (напрямую из A) + 1 (через B) + 2 (через C) = 4
Шаг 4: Теперь выполним подсчёт путей из A в E:
2 (через C) + 4 (через D) = 6
Ответ: 6 различных путей.
⚡ Лайфхак
Решение задачи будет гораздо проще, если двигаться от вершины A (начало маршрута) к вершине E и проставлять веса вершин — число путей из A в текущую вершину. При этом вес вершины A можно принять за 1. Действительно, существует единственный способ попасть из A в A — оставаться на месте.
🚣 Пример 2: Задача о переправе
Рассмотрим несколько видоизменённую классическую задачу о переправе.
📖 Условие задачи
На берегу реки стоит крестьянин (К) с лодкой, а рядом с ним — собака (С), лиса (Л) и гусь (Г). Крестьянин должен переправиться сам и перевезти собаку, лису и гуся на другой берег.
Однако в лодку, кроме крестьянина, помещается либо только собака, либо только лиса, либо только гусь. Оставлять же собаку с лисой или лису с гусём без присмотра крестьянина нельзя: собака представляет опасность для лисы, а лиса — для гуся.
Как крестьянин должен организовать переправу?
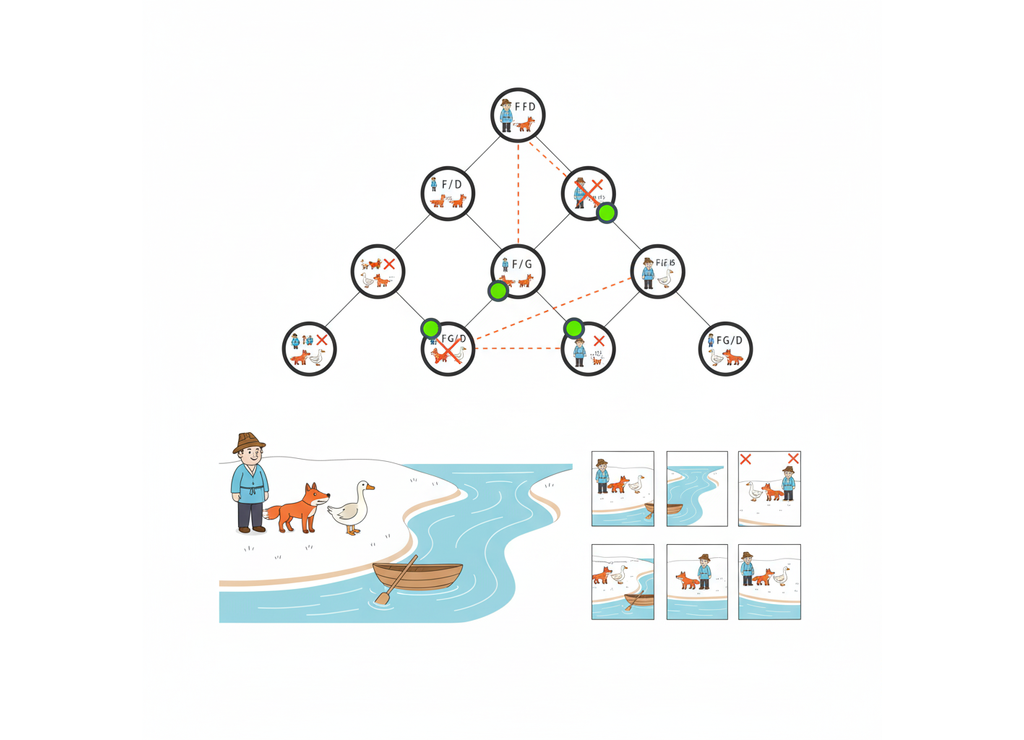
Граф переправы (дерево решений)
💡 Решение
Для решения этой задачи составим граф, вершинами которого будут исходное и результирующее размещение персонажей на берегах реки, а также всевозможные промежуточные состояния, достигаемые из предыдущих за один шаг переправы.
Каждую вершину-состояние переправы обозначим овалом и свяжем рёбрами с состояниями, образованными из неё.
- Непустимые по условию задачи состояния выделены пунктирной линией
- Начальное и конечное состояния переправы выделены жирной линией
✅ План переправы (одно из решений)
- Крестьянин перевозит лису
- Крестьянин возвращается
- Крестьянин перевозит собаку
- Крестьянин возвращается с лисой
- Крестьянин перевозит гуся
- Крестьянин возвращается
- Крестьянин перевозит лису
На графе видно, что существуют два решения этой задачи!
💡 Вывод
С помощью графов можно решать и разные занимательные задачи!
2.3.3. Деревья
Дерево — это связный граф, в котором нет циклов, т.е. в нём нельзя из некоторой вершины пройти по нескольким различным рёбрам и вернуться в ту же вершину.
🎯 Ключевое свойство дерева
Отличительной особенностью дерева является то, что между любыми двумя его вершинами существует единственный путь.
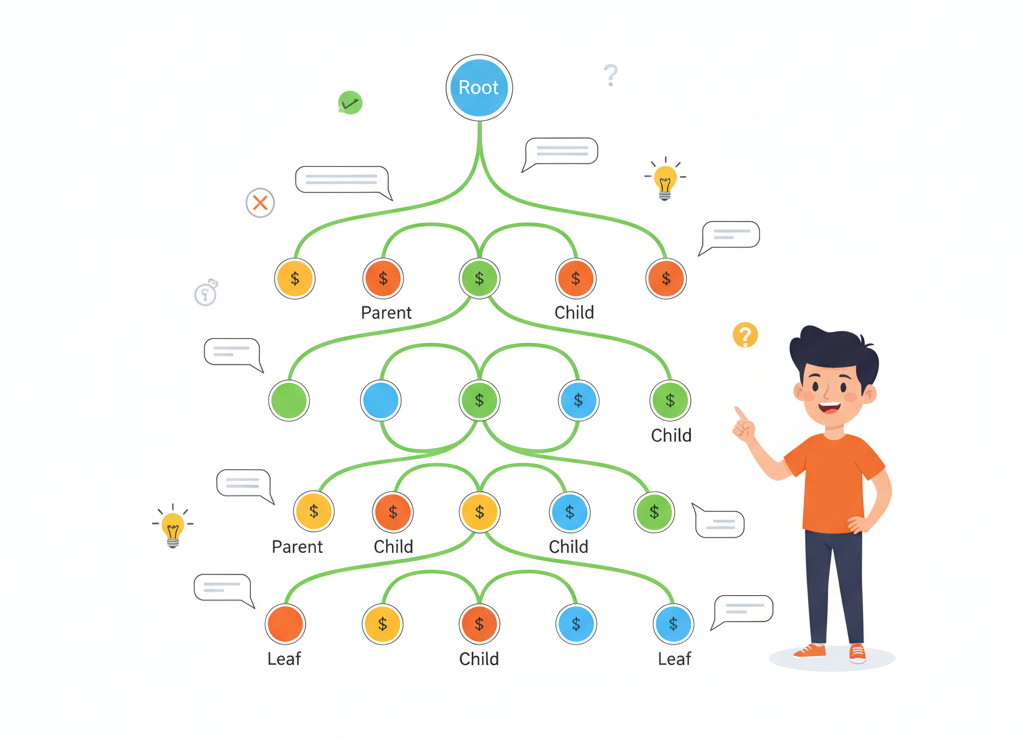
Пример дерева с корнем, предками, потомками и листьями
Основные понятия
🌳 Главная вершина
У дерева выделяется одна главная вершина, называемая его корнем
⬆️ Родительская вершина
Каждая вершина (кроме корня) имеет единственного предка; корень предка не имеет
⬇️ Дочерние вершины
Любая вершина дерева может порождать несколько потомков
🍃 Конечные вершины
Вершины, не имеющие порождённых вершин (потомков), называют листьями
🌿 Часть дерева
Любая вершина дерева вместе со всеми своими вершинами-потомками
📊 Расстояние от корня
Длина пути от корня до вершины; уровень корня равен нулю
📏 Максимальная глубина
Максимальный уровень вершин, образующих дерево (наибольшая длина пути от корня к листу)
🔍 Проверь себя
Внимательно рассмотри дерево на рисунке выше и ответь на вопросы:
- Сколько у этого дерева вершин?
- Какова высота этого дерева?
- Приведи пример поддерева в этом дереве
- Приведи примеры вершин 1-го, 2-го, 3-го и 4-го уровня
🏛️ Применение деревьев
Всякая иерархическая система может быть представлена с помощью дерева.
Родственные связи между членами семьи удобно изображать с помощью графа, называемого генеалогическим или родословным деревом.
🌳 Пример 3: Дерево вариантов
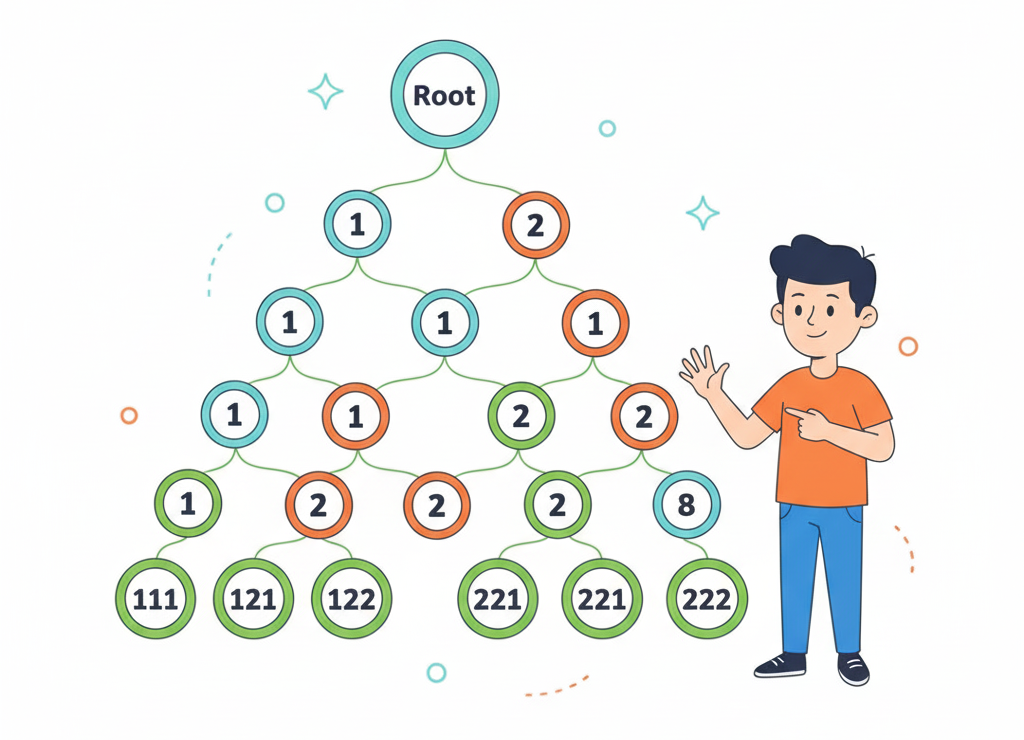
Для того чтобы записать все трёхзначные числа, состоящие из цифр 1 и 2, можно построить дерево вариантов.
Дерево вариантов для решения задачи о записи трёхзначных чисел
💡 Решение без построения дерева
Дерево можно не строить, если не требуется выписывать все возможные варианты, а нужно просто указать их количество. В этом случае рассуждать нужно так:
- В разряде сотен может быть любая из цифр 1 и 2
- В разряде десятков — те же два варианта
- В разряде единиц — те же два варианта
Число различных вариантов: 2 · 2 · 2 = 8
📐 Правило перемножения
В общем случае, если известно количество возможных вариантов выбора на каждом шаге построения графа, то для вычисления общего количества вариантов нужно все эти числа перемножить.
🎮 Пример 4: Дерево игры
Рассмотрим следующую игру: сначала в кучке лежат 5 спичек; два игрока убирают спички по очереди, причём за 1 ход можно убрать 1 или 2 спички; выигрывает тот, кто оставит в кучке 1 спичку. Выясним, кто выигрывает при правильной игре — первый (I) или второй (II) игрок.
Дерево игры (все возможные варианты ходов)
🎯 Анализ игры
Ход игрока I: Может убрать одну спичку (останется 4) или сразу 2 (останется 3).
Если останется 4 спички: Игрок II может своим ходом оставить 3 или 2 спички.
Если останется 3 спички: Игрок II может выиграть, взяв две спички и оставив одну.
Если после хода игрока II осталось 3 или 2 спички: Игрок I в каждой из этих ситуаций имеет шанс на выигрыш.
✅ Вывод
Таким образом, при правильной стратегии игры всегда выигрывает первый игрок. Для этого своим первым ходом он должен взять одну спичку.
🎲 Что такое дерево игры?
На рисунке представлен граф, называемый деревом игры; на нём отражены все возможные варианты, в том числе ошибочные (проигрышные) ходы игроков.
Дерево игры — один из вариантов игровых моделей, используемых при моделировании действий противоборствующих сторон в ходе соревнований, конкуренции в бизнесе и даже военных действий.
Игровые модели позволяют разработать план действий, обеспечивающий самый лучший результат за счёт учёта возможных действий противника.
📌 САМОЕ ГЛАВНОЕ
🤔 Проверь себя
Проверь, как хорошо ты усвоил материал!
1. Какие информационные модели относят к графическим?
Вспомни: схемы, карты, чертежи, графики, диаграммы, графы.
2. Приведи примеры графических информационных моделей, с которыми ты имеешь дело
а) при изучении других предметов:
- Физика: схемы электрических цепей
- География: географические карты
- Биология: схемы строения организмов
- История: карты военных действий
б) в повседневной жизни:
- Карты в навигаторе (Яндекс.Карты, 2ГИС)
- Схемы метро
- Графики курсов валют
- Диаграммы в соцсетях (статистика)
3. Что такое граф? Приведи примеры цепей и циклов
Граф — это структура, состоящая из вершин, соединённых линиями (рёбрами или дугами).
На рис. 2.10, в вершины — это пункты A, B, C, D, E; рёбра — дороги между ними с указанием расстояния.
Задание: Определи, какие два пункта наиболее удалены друг от друга. Укажи длину кратчайшего пути между этими пунктами.
4. Приведи пример системы, модель которой можно представить в форме графа
Примеры:
- Социальная сеть (вершины — пользователи, рёбра — дружеские связи)
- Транспортная сеть города (вершины — остановки, рёбра — маршруты)
- Интернет (вершины — сайты, рёбра — гиперссылки)
- Структура компании (вершины — сотрудники, рёбра — подчинённость)
5. Задача про велосипедиста
Условие: Грунтовая дорога проходит последовательно через населённые пункты A, B, C и D. При этом длина грунтовой дороги между A и B равна 40 км, между B и C — 25 км, между C и D — 10 км. Между A и D дороги нет. Между A и C построили новое асфальтовое шоссе длиной 30 км.
Оцени минимально возможное время движения велосипедиста из пункта A в пункт B, если его скорость по грунтовой дороге — 20 км/ч, по шоссе — 30 км/ч.
Подсказка: Сравни два варианта: напрямую по грунтовой дороге и через новое шоссе.
6. Задача: сколько существует различных путей от точки A до точки G?
На рисунке изображена схема дорог, связывающих торговые точки A, B, C, D, E, F, G. По каждой дороге можно двигаться только в направлении, указанном стрелкой.
Совет: Используй метод взвешенного графа, который мы разбирали в примере 1!
7. Составь семантическую сеть по русской народной сказке
Задание для работы в группе: Выбери одну из сказок: «Колобок», «Курочка Ряба», «Репка».
Создай граф, где вершины — персонажи и объекты, а рёбра — отношения между ними (например, "встретил", "съел", "тянул", "помог").
8. Что такое дерево? Моделями каких систем могут служить деревья?
Дерево — это связный граф без циклов, в котором между любыми двумя вершинами существует единственный путь.
Примеры систем:
- Генеалогическое (семейное) дерево
- Файловая система компьютера
- Структура сайта
- Организационная структура компании
- Классификация живых организмов
9. Сколько трёхзначных чисел можно записать с помощью цифр 2, 4, 6 и 8?
Условие: В записи числа не должно быть одинаковых цифр.
Подсказка: Используй правило перемножения или построй дерево вариантов!
10. Сколько существует трёхзначных чисел, все цифры которых различны?
Подсказка:
- На первое место можно поставить 9 цифр (кроме 0)
- На второе — любую из оставшихся 9
- На третье — любую из оставшихся 8
11. Задача про цепочки из бусин
Для составления цепочек используются бусины, помеченные буквами A, B, C, D, E.
Правила:
- На первом месте в цепочке стоит одна из бусин A, C, E
- На втором — любая гласная, если первая буква гласная, и любая согласная, если первая согласная
- На третьем месте — одна из бусин C, D, E, не стоящая в цепочке на первом месте
Вопрос: Сколько цепочек можно создать по этому правилу?
12. Задача про Вычислитель
У исполнителя Вычислитель две команды, которым присвоены номера:
- 1 — прибавь 1
- 2 — умножь на 3
Выполняя первую из них, Вычислитель прибавляет к числу на экране 1, а выполняя вторую, утраивает это число.
Вопросы:
- Какое максимальное количество разных программ, состоящих из пяти команд, можно составить для этого исполнителя?
- Пусть 0 — начальное значение. Какие числа будут получены в результате выполнения всех программ для исполнителя Вычислитель, состоящих не более чем из четырёх команд?
- Решение оформи в виде дерева. Какое наибольшее число будет записано в вершинах третьего уровня?
13. Представь отношения между множествами в форме дерева
Задание: Используй диаграмму Эйлера из задания 13 учебника.
- Сколько у этого дерева вершин?
- Какова высота этого дерева?
- Приведи пример поддерева
- Приведи примеры листьев. Вершинами какого уровня они являются?
14. Задача про игроков и камни
Условие: Два игрока играют в следующую игру. Перед ними лежит куча из 6 камней. Игроки берут камни по очереди. За один ход можно взять 1, 2 или 3 камня. Проигрывает тот, кто забирает последний камень.
Вопросы:
- Кто выигрывает при безошибочной игре обоих игроков — игрок, делающий первый ход, или игрок, делающий второй ход?
- Каким должен быть первый ход выигрывающего игрока?
- Ответ обоснуй, построив дерево игры
🎯 Практические задания
Попробуй применить полученные знания на практике!
🗺️ Задание 1: Построй граф
Нарисуй граф своих друзей в соцсети (возьми 5-7 человек). Обозначь:
- Вершины — имена друзей
- Рёбра — кто с кем дружит
Дополнительно: Является ли этот граф связным? Есть ли в нём циклы?
🚇 Задание 2: Анализируй маршрут
Возьми схему метро своего города (или любого другого). Найди кратчайший путь между двумя станциями, используя знания о графах.
Усложнение: Учти время пересадок!
🌳 Задание 3: Построй дерево
Составь генеалогическое дерево своей семьи (минимум 3 поколения):
- Определи корень дерева
- Укажи уровни вершин
- Найди все листья
- Какова высота твоего дерева?
🎲 Задание 4: Реши задачу
Измени условие задачи о спичках: теперь в кучке 7 спичек, можно брать 1, 2 или 3 спички. Выигрывает тот, кто берёт последнюю.
Построй дерево игры и определи выигрышную стратегию!