Таблицы истинности: как разгадать любую логическую головоломку
Сейчас мы узнаем, как превратить запутанные логические высказывания в понятные таблицы — настоящий лайфхак для решения задач!

Как построить таблицу истинности
Давайте представим: ты играешь в игру, где нужно предсказать все возможные исходы. У тебя есть несколько условий (переменных), и ты хочешь знать, что получится при каждой их комбинации. Именно для этого и придумали таблицы истинности!
💡 Определение
Таблица истинности логического выражения — это таблица, которая показывает, какие значения принимает выражение при всех возможных наборах значений входящих в него переменных.
Представь, что это чит-таблица для логики: вбиваешь все варианты — получаешь все ответы.
🎯 Как её построить: пошаговый план
Построение таблицы истинности — это алгоритм из восьми простых шагов.
Восемь шагов — и таблица готова!
Подсчитай переменные
Сколько букв (A, B, C и т.д.) в твоём выражении? Это число обозначим как n.
Установи порядок операций
Вспомни про скобки и приоритеты (сначала конъюнкция ∧, потом дизъюнкция ∨). Как в математике: сначала умножение, потом сложение.
Посчитай операции
Сколько раз ты будешь что-то вычислять? Это важно для количества столбцов.
Определи количество столбцов
Столбцов будет: n (переменные) + количество операций.
Заполни шапку
Впиши переменные и операции по порядку.
Определи количество строк
Формула магическая: m = 2n. Если две переменные — 4 строки, три переменные — 8 строк. Просто возводи двойку в степень!
Заполни входные данные
Наборы значений — это все комбинации 0 и 1. Они идут как двоичные числа от 0 до 2n − 1:
- Для n=2: 00, 01, 10, 11
- Для n=3: 000, 001, 010, 011, 100, 101, 110, 111
Заполни результаты
Теперь просто выполняй логические операции по порядку для каждой строки. Идёшь столбец за столбцом — как в судоку!
Пример 1: Строим таблицу для выражения A ∨ A ∧ B
Давай разберём на конкретном примере. У нас выражение A ∨ A ∧ B.
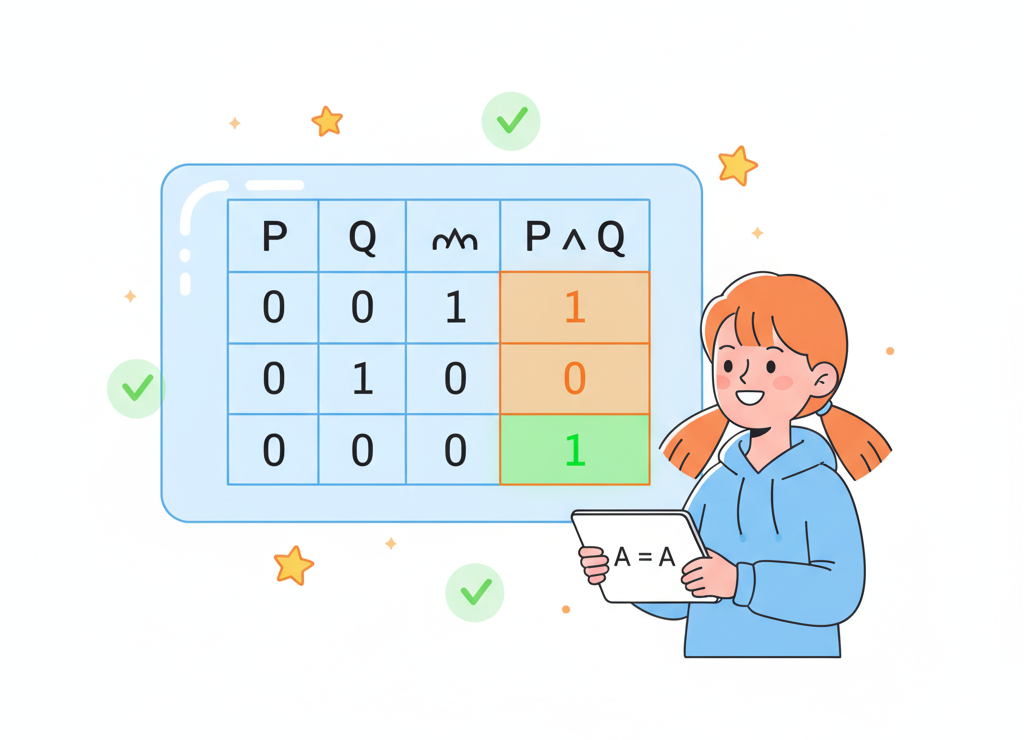
Таблица показала, что сложное выражение можно упростить!
🔍 Что у нас есть?
- Две переменные: A и B
- Две операции: сначала конъюнкция (∧), потом дизъюнкция (∨)
- Значит, в таблице будет 4 столбца: A, B, A ∧ B, A ∨ A ∧ B
✨ Обрати внимание!
Последний столбец (результат) совпал со столбцом A! Это значит, что выражение A ∨ A ∧ B на самом деле равносильно просто переменной A. Круто, правда? Мы только что упростили сложное выражение!
Законы алгебры логики через таблицы
С помощью таблиц истинности можно доказывать различные свойства логических операций — это называется законы алгебры логики.
Когда столбцы совпадают — закон доказан!
Пример 2: Распределительный закон
Давай докажем, что: A ∨ (B ∧ C) = (A ∨ B) ∧ (A ∨ C)
Это как в математике: вынести за скобку. Только здесь — логика!
У нас три переменные (A, B, C), значит, строк будет 2³ = 8. Построим большую таблицу:
🎯 Вывод
Смотри: столбцы A ∨ (B ∧ C) и (A ∨ B) ∧ (A ∨ C) полностью совпадают! Значит, распределительный закон работает. Мы его только что доказали!
Решаем логические задачи с помощью таблиц
Часто бывает так, что нужно не просто построить таблицу, а решить настоящую головоломку. Давай посмотрим, как это работает!

Кто виноват? Логика поможет найти ответ!
Задача про бабушкину вазу
📖 Условие
Коля, Вася и Серёжа гостили летом у бабушки. Однажды один из мальчиков нечаянно разбил любимую бабушкину вазу. На вопрос, кто разбил вазу, они дали такие ответы:
- Серёжа: 1) я не разбивал; 2) Вася не разбивал.
- Вася: 3) Серёжа не разбивал; 4) вазу разбил Коля.
- Коля: 5) я не разбивал; 6) вазу разбил Серёжа.
Бабушка знала, что один из её внуков всегда говорит правду (назовём его правдивым), один всегда врёт (шутником), а третий один раз сказал правду, а другой — неправду (хитрецом).
Вопрос: Кто из внуков разбил вазу? Назови имена правдивого, шутника и хитреца.
Решение
Шаг 1. Введём переменные
Пусть:
- K = «Коля разбил вазу»
- B = «Вася разбил вазу»
- C = «Серёжа разбил вазу»
Так как вазу разбил только один внук, достаточно рассмотреть комбинации: 001, 010, 100 (в двоичной записи).
Шаг 2. Построим таблицу
Для каждого высказывания мальчиков запишем его в виде логического выражения:
Шаг 3. Ищем нужную строку
Нам нужна строка, где в каком-то порядке встречаются три комбинации:
- 00 — слова шутника (обе лжи)
- 11 — слова правдивого внука (обе правды)
- 01 или 10 — слова хитреца (одна правда, одна ложь)
Анализируя первую строку (K=0, B=0, C=1), видим:
- Серёжа: 0, 1 — хитрец
- Вася: 0, 0 — шутник
- Коля: 1, 1 — правдивый!
Эта строка подходит!

Логика — лучший детектив!
✅ Ответ
Вазу разбил Серёжа. Коля — правдивый внук, Вася — шутник, Серёжа — хитрец.
Самое главное
Подведём итоги того, что мы узнали о таблицах истинности.
🤔 Проверь себя
Проверь, как хорошо ты усвоил материал!
1. Построй таблицы истинности для следующих выражений
Задания:
- а) B ∧ (A ∨ B)
- б) A ∧ (B ∨ B̄)
- в) B ∧ (A ∨ B ∨ C)
- г) A ∧ B ∨ C̄
Подсказка: начни с подсчёта переменных и определения количества строк!
2. Докажи с помощью таблиц истинности справедливость следующих тождеств (законы де Моргана)
Задания:
- а) Ā ∨ B̄ = A̅ ∧̅ B̅
- б) Ā ∧ B̄ = A̅ ∨̅ B̅
Построй таблицы для левой и правой части — если столбцы совпадут, тождество доказано!
3. Сколько строк будут содержать таблицы истинности для следующих выражений?
Задания:
- а) A ∧ B ∧ C
- б) A ∧ B ∧ C ∧ D
- в) A ∨ B ∨ C
- г) A ∨ B ∨ C ∨ D
Дополнительный вопрос: Для каких наборов значений переменных эти выражения истинны?
Попробуй ответить без построения полной таблицы — подумай логически!
4. Логическая олимпиада — кто прошёл на городской тур?
В школьной олимпиаде по информатике приняли участие три ученика 8 класса: Александр, Иван и Мария. Перед олимпиадой их друзья высказали три предположения:
- Александр сможет пройти на городской тур олимпиады, или Иван не сможет пройти на городской тур олимпиады.
- Иван сможет пройти на городской тур олимпиады.
- Неверно, что Мария и Александр смогут пройти на городской тур олимпиады.
Вопрос: Кто из ребят прошёл на городской этап олимпиады, если все предположения оказались истинными высказываниями?
Подсказка: обозначь «Александр прошёл» как A, «Иван прошёл» как I, «Мария прошла» как M, построй таблицу и ищи строку, где все три высказывания истинны!
5. Придумай свою задачу!
Создай логическую головоломку про трёх друзей, которые что-то сделали (например, купили пиццу, посмотрели фильм или выиграли в игру).
Условия:
- Пусть каждый даст по два утверждения
- Один всегда говорит правду
- Один всегда врёт
- Один иногда врёт, иногда правду
Попробуй решить её с помощью таблицы истинности! Затем дай решить другу.
6. Как ты думаешь, где в реальной жизни используются таблицы истинности?
Подсказка: подумай о компьютерных схемах, программировании, базах данных, поисковых системах...
7. Представь, что тебе нужно объяснить другу, что такое таблица истинности. Как ты это сделаешь?
Попробуй объяснить простыми словами, используя понятные примеры из жизни.
🎯 Практические задания
Попробуй применить полученные знания на практике!
✍️ Задание 1: Быстрая таблица
Построй таблицу истинности для выражения A ∧ B̄ (A и НЕ B).
Сколько строк у тебя получилось? Для каких наборов значений выражение истинно?
🔍 Задание 2: Найди упрощение
Построй таблицу истинности для выражения A ∨ (A ∧ B).
Можно ли его упростить? Какой переменной равносильно это выражение?
🎨 Задание 3: Три переменных
Построй таблицу истинности для выражения A ∧ B ∧ C.
Когда конъюнкция трёх переменных будет истинной? Сколько строк в таблице?
🔄 Задание 4: Проверка закона
Докажи с помощью таблицы, что A ∧ 1 = A (закон нейтрального элемента для конъюнкции).
Что будет, если заменить 1 на 0?